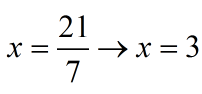Matemáticas para la vida trigonometria
Relación entre los lados y los ángulos de un triangulo
Existe una estrecha relación entre
los lados y los ángulos de un triangulo, esta relación es muy útil para
resolver problemas de la vida diaria, veamos un ejemplo de la resolución de un
problema en el que usando las matemáticas se resuelve muy fácilmente y que sin
la ayuda de ellas sería muy difícil, ya que necesitaríamos de equipo especial.
Supongamos que necesitamos
conocer la altura de un edificio. ¿Cómo lo podríamos medir?
Resolución usando la relaciones
que existen en los triángulos.
1: podemos medir la sombra que
proyecta el edificio.
Ese edificio, a determinada hora
del día proyecta una sombra de 50m
Una varilla de 1m a la misma hora
del dia proyecta una sombra de 1.8m
En la siguiente figura está en
color gris la proyección de la sombra, llamaremos x el valor desconocido.
Con los datos conocidos
realizamos la siguiente proporción y la resolvemos mediante una regla de tres
simple.
El edificio mide 27.78 metros.
En este ejemplo tomamos la medida
de una varilla que bien nosotros pudimos preparar, pero en realidad podemos
utilizar cualquier cosa que podamos medir. Debemos tomar en cuenta que la
medida que obtuvimos fue a una hora determinada y que esta medida cambia con la
hora del dia y también con las estaciones del año.
Si te gusto este articulo compártelo.
Si te gusto este articulo compártelo.