Resolución de sistemas de ecuaciones lineales : método de igualación
Este método se basa en despejar
una de las incógnitas en las dos ecuaciones para posteriormente igualar estas
expresiones y obtener el valor numérico de una de estas incógnitas para
continuar sustituyendo ese valor en la ecuación más sencilla y así obtener el
valor numérico de la otra incógnita.
Podemos seguir los siguientes
pasos para resolver un sistema de ecuaciones lineales por este método.
1: si es posible simplificamos
las o una de las ecuaciones.
2: despejamos una de las
incógnitas en las dos ecuaciones.
3: igualamos estas expresiones.
4: resolvemos la ecuación de
primer grado con una incógnita que obtuvimos de esta igualación ( Ver como
resolver ecuaciones de primer grado con fracciones).
5: ya obtenido el valor numérico de
esta incógnita, lo sustituimos en la ecuación más sencilla.
6: resolvemos la nueva ecuación de
primer grado con una incógnita para obtener el valor numérico de la incógnita.
Ahora tenemos los valores numéricos
de (x,y) que satisfacen el sistema.
Ejemplo.
Resolvemos el siguiente sistema
de ecuaciones lineales con el método de igualación.
Despejamos x en las dos
ecuaciones (En este caso no se podía simplificar ninguna de las dos
ecuaciones).
Igualamos las expresiones
obtenidas para tener una ecuación de primer grado con una incógnita.
Resolvemos esta ecuación para
obtener el valor numérico de y (ver como resolver ecuaciones de primer grado
con fracciones).
Ya con el valor numérico de y, lo
sustituimos en la ecuación mas sencilla.
Resolvemos esta nueva ecuación de
primer grado con una incógnita (ver resolución de ecuaciones de primer grao).
Ahora tenemos los valores de
(x,y) que satisfacen el sistema.
Comprobamos sustituyendo estos
valores en el sistema y comprobando si la igualdad es correcta.
Continua aprendiendo.
Resolución de sistemas método de reducción
Resolución de sistemas método de sustitución
Resolución de sistemas método de reducción
Resolución de sistemas método de sustitución






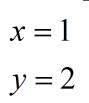




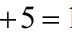

Es un método sencillo y comprensible para los estudiantes, me parece que lo que sigue es aterrizarles fisicamente sobre lo que puede significar cada término. Gracias
ResponderBorrarRobinson Ramírez A.